

(2017/2º Semestre/Questão 20) Um marido apaixonado resolveu prestar uma homenagem à sua esposa, construindo um jardim em forma de coração por meio de um quadrado e dois semicírculos, conforme a figura. Para construí-lo, ele usou mudas de flores vermelhas na razão de 200 mudas por metro quadrado. Assim, o total de mudas utilizadas na montagem de tal jardim foi de (Considere π=3).
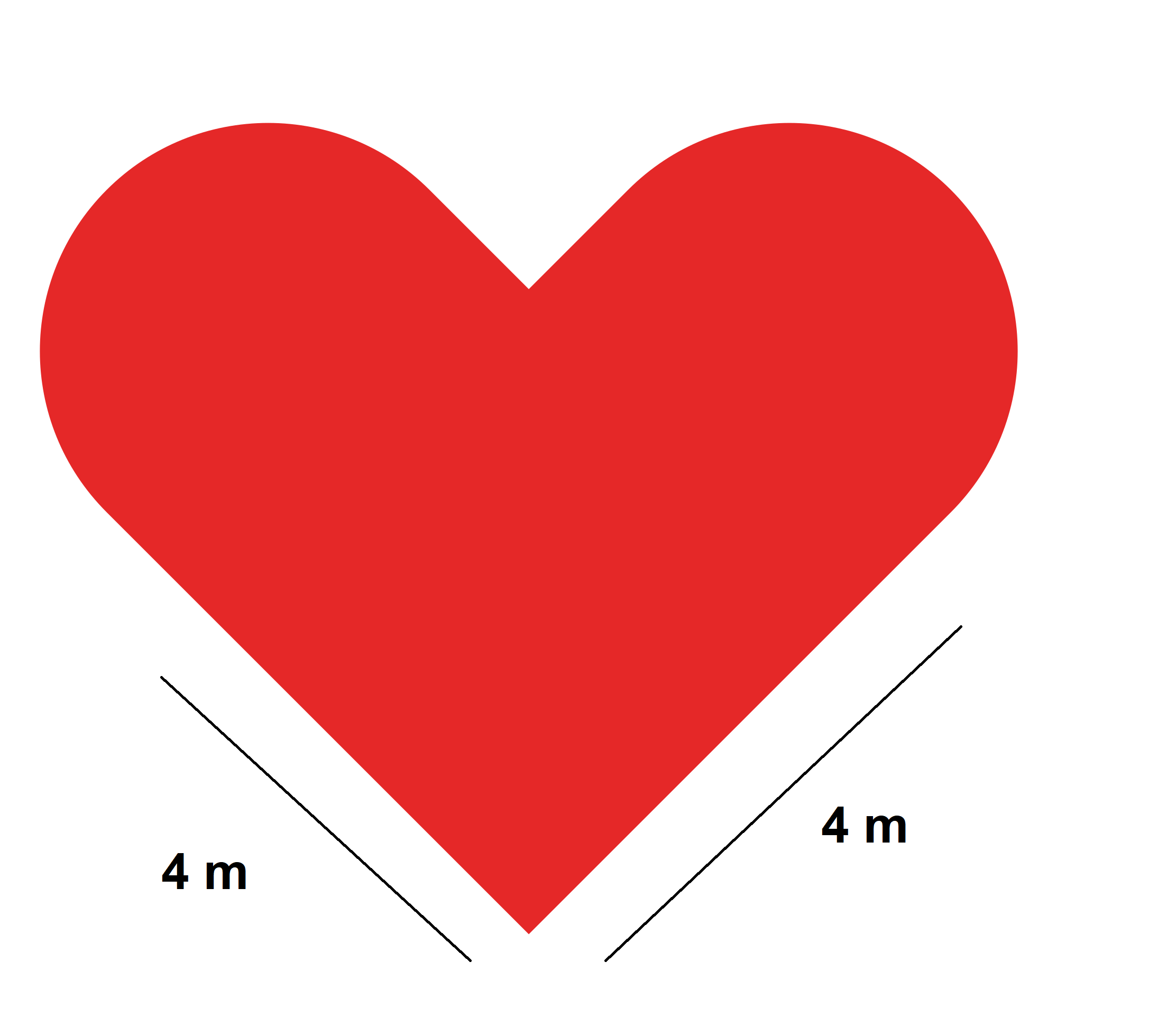
A) 3200
B) 5600
C) 8000
D) 9600
(2016/2º semestre/Questão 17) João comprou um presente para sua esposa Maria e parcelou a compra da seguinte maneira: a primeira parcela foi de R$50,00, a segunda de R$52,00, a terceira de R$54,00 e assim sucessivamente até a última parcela de R$100,00. O valor total do presente é:
A) R$256,00
B) R$512,00
C) R$1950,00
D) R$2025,00
(2015/2º semestre/Questão 21) Em um grupo de pessoas, 64 conhecem a cidade de Poços de Caldas e 60 conhecem Pouso Alegre. Neste grupo 24 pessoas conhecem essas duas cidades. Se sortearmos ao acaso uma dessas pessoas, a possibilidade de que ela só conheça Poços de Caldas é:
A) 0,4
B) 0,6
C) 0,24
D) 0,36
(2017/2º Semestre/Questão 19) Uma famosa região rodeada por mistérios é o Triângulo das Bermudas, localizado entre a ilha Bermudas, Miami e San Juan (Porto Rico), que possuem como coordenadas aproximadas, respectivamente, (10,-4), (3,-20) e (-4,-6), dadas em graus (Latitude, Longitude). Considerando as coordenadas dadas para o Triângulo das Bermudas, a área dessa região em graus quadrados será de:
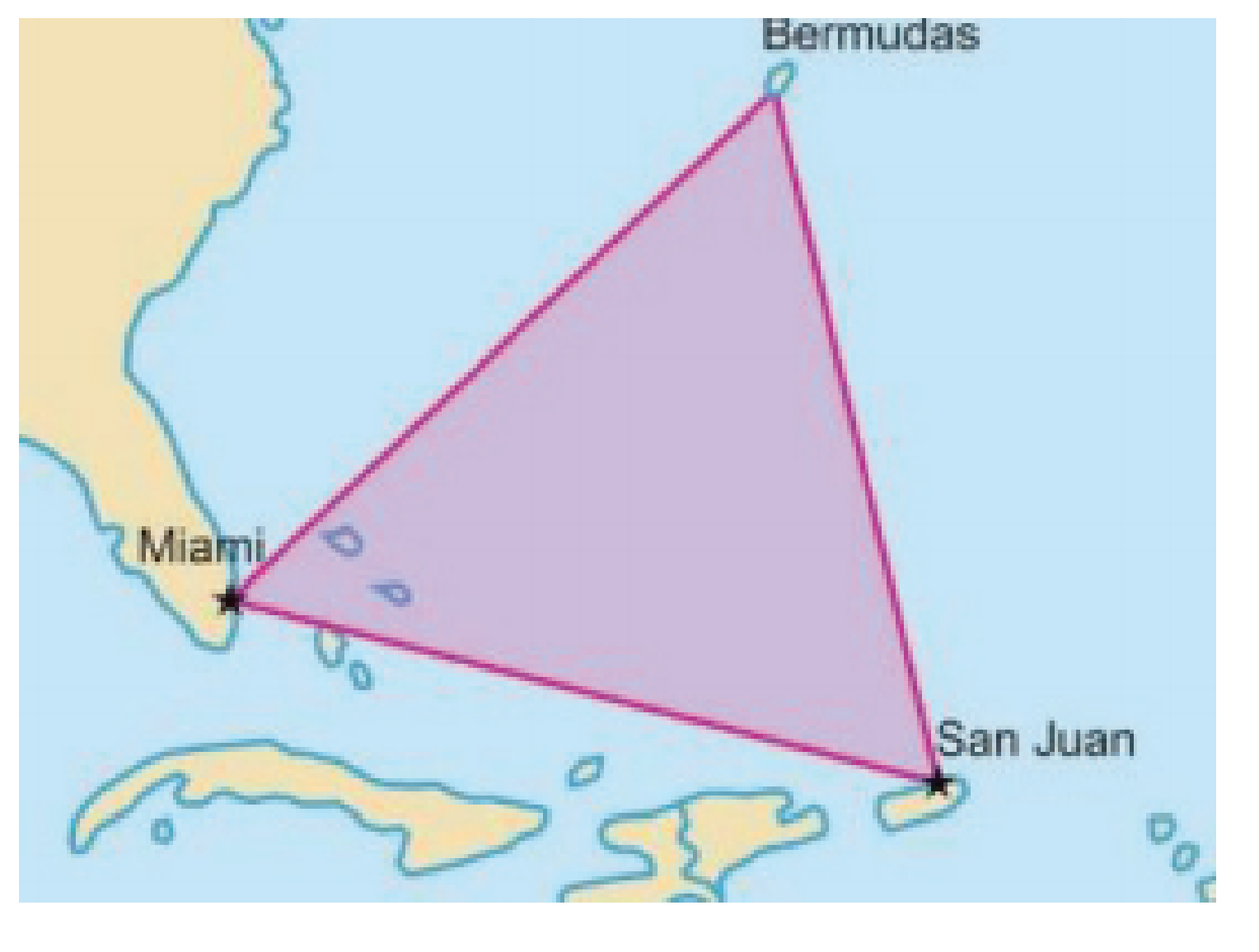
A) 270
B) 210
C) 105
D) 47
(2016/2º semestre/Questão 19) Um engenheiro precisava medir o comprimento de um pedaço da parede de um prédio. Como esse pedaço estava muito alto, ele decidiu realizar a seguinte estratégia: pegou uma escada de 25m e a encostou em um ponto A do prédio e mediu a distância do pé da escada até o prédio que deu 20m. Depois inclinou a escada até alcançar o ponto B no prédio, mais alto do que A, e mediu novamente a distância do pé da escada até o prédio que deu 7m. Desse modo, o engenheiro concluiu que a distância entre o ponto A e o B deu:
A) 13m
B) 11m
C) 9m
D) 7m
(2015/2º semestre/Questão 22) Um primeiro cilindro possui raio r e altura h. Um segundo cilindro possui o raio 2r e altura h/2. Nestas condições sobre o volume de cada um destes cilindros, é CORRETO afirmar que:
A) Os seus volumes são iguais.
B) O volume do segundo é 4 e o volume do primeiro é 1.
C) O volume do primeiro é o quádruplo do volume do segundo.
D) O volume do segundo é dobro do volume do primeiro.
(2018/Questão 23) O volume de um tetraedro regular de aresta 1cm é igual a:
A) √2/12
B) √3/4
C) √2/6
D) √3/8
(2018/Questão 25) Qual o menor ângulo formado pelos ponteiros de um relógio quando este marca 12 h e 20 min?
A) 120º
B) 110º
C) 100º
D) 90º
(2017/1º Semestre/Questão 17) Observe a seguinte tirinha:

De fato, o filho usou uma interpretação incorreta para tentar ludibriar seu pai e ganhar um tablet. Colocando os dados apresentados pelo filho em um único gráfico, o resultado obtido será:
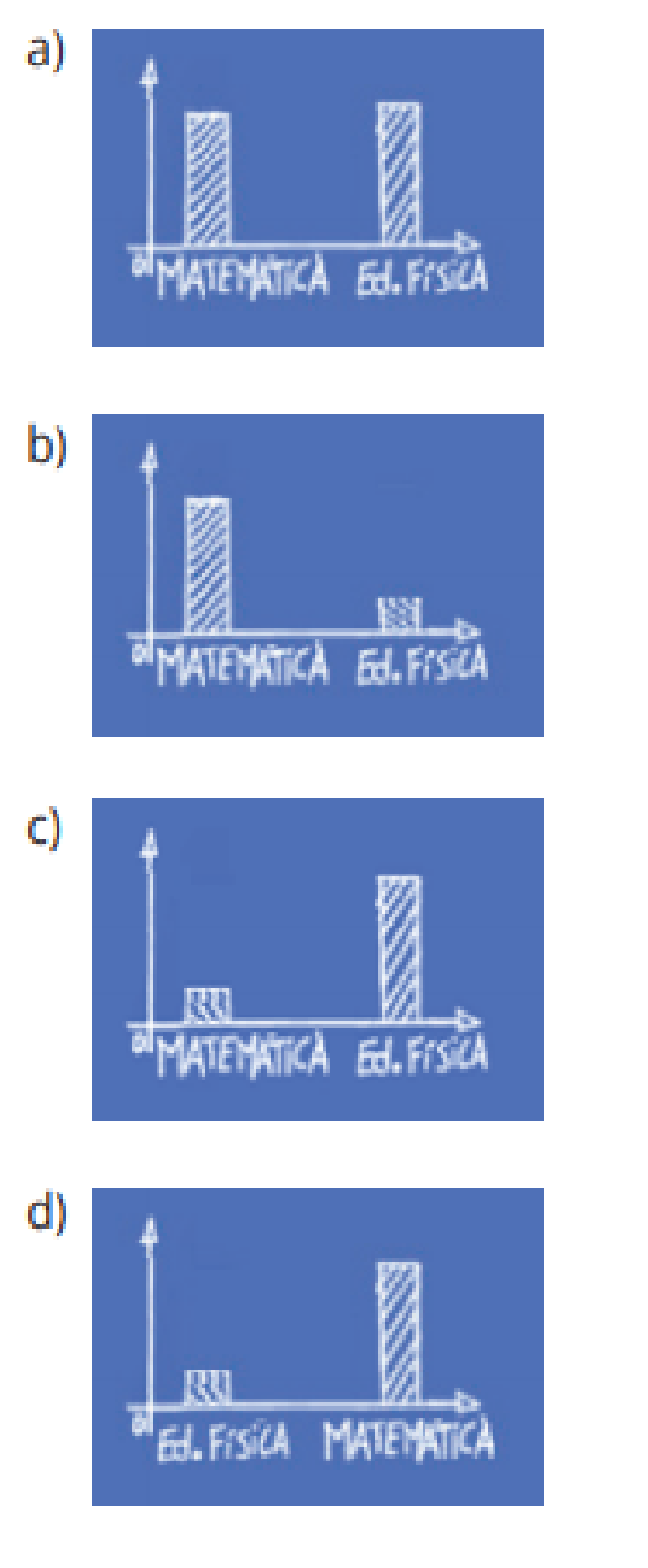
(2016/2º semestre/Questão 21) Um programador decidiu estabelecer um critério para criação de senhas para seu programa de administração de uma farmácia. Ela deveria ser formada pelos seguintes números: {1,2,4,5,6,8,9,0}, ter três algarismos diferentes e ser múltiplo de cinco. A quantidade de senhas que poderão ser criadas será:
A) 78
B) 84
C) 5040
D) 40320
(2018/Questão 19) Lançando-se simultaneamente dois dados não viciados, a probabilidade de que suas faces superiores exibam soma igual a 7 ou a 9 é:
A) 1/6
B) 5/6
C) 5/18
D) 5/36
(2015/2º semestre/Questão 19) Em um campeonato amador de futebol 20 equipes participaram. Cada equipe jogou com cada uma das outras equipes duas vezes. De acordo com esta regra o número total de partidas neste campeonato é:
A) 20
B) 40
C) 190
D) 380
(2016/2º semestre/Questão 23)Um aluno do IFSULDEMINAS estava estudando números complexos e achou muito estranho que o produto ou a soma de um número complexo com o seu conjugado pudesse ter como resultado um número real. Então resolveu testar com o seguinte número complexo z = 3 + 2i. Qual o resultado que o aluno encontrou para o produto e a soma respectivamente?
A) 13 e 6
B) 5 e 5
C) 6 - 4i e 6
D) 6 - 4i e 9 - 4i
(2015/2º semestre/Questão 25) O gráfico de uma função afim que passa pelos pontos P(1; 1) Q(2; 2). Podemos afirmar que a sua lei de formação que define esta função é:
A) f(x)= x + 1
B) f(x)= x
C) f(x)= 2x
D) f(x)= x + 2
(2015/2º semestre/Questão 18) Um triângulo tem os seus vértices nos pontos de coordenadas A(5;1), B(1;1) e C(1;2). Se a distância que une os vértices deste triângulo é dada em metros então, pode-se afirmar que a área delimitada por este triângulo vale:
A) 2 metros quadrados
B) 4 metros quadrados
C) 6 metros quadrados
D) 8 metros quadrados