

Fuvest 2018/01 Primeira Fase
24- Em uma urna, há bolas amarelas, brancas e vermelhas. Sabe se que: I. A probabilidade de retirar uma bola vermelha dessa urna é o dobro da probabilidade de retirar uma bola amarela. II. Se forem retiradas 4 bolas amarelas dessa urna, a probabilidade de retirar uma bola vermelha passa a ser 1/2. Se forem retiradas 12 bolas vermelhas dessa urna, a probabilidade de retirar uma bola branca passa a ser 1/2.
A quantidade de bolas brancas na urna é :
A) 8
B) 10
C) 12
D) 14
E) 16
26- Doze pontos são assinalados sobre quatro segmentos de reta de forma que três pontos sobre três segmentos distintos nunca são colineares, como na figura.
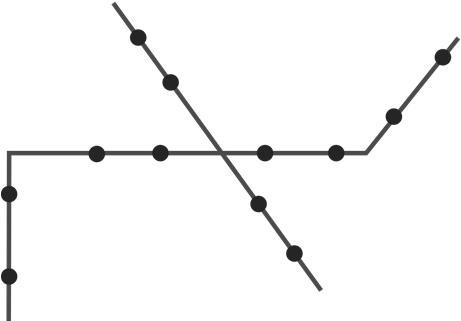
O número de triângulos distintos que podem ser desenhados com os vértices nos pontos assinalados é
A) 200
B) 204
C) 208
D) 212
E) 220
27- Dentre os candidatos que fizeram provas de matemática, português e inglês num concurso, 20 obtiveram nota mínima para aprovação nas três disciplinas. Além disso, sabe-se que: I. 14 não obtiveram nota mínima em matemática; II. 16 não obtiveram nota mínima em português; III. 12 não obtiveram nota mínima em inglês; IV. 5 não obtiveram nota mínima em matemática e em português; V. 3 não obtiveram nota mínima em matemática e em inglês; VI. 7 não obtiveram nota mínima em português e em inglês VII. 2 não obtiveram nota mínima em português, matemática e inglês. A quantidade de candidatos que participaram do concurso foi
A) 44
B) 46
C) 47
D) 48
E) 49
31- Maria quer comprar uma TV que está sendo vendida por R$ 1.500,00 à vista ou em 3 parcelas mensais sem juros de R$ 500,00. O dinheiro que Maria reservou para essa compra não é suficiente para pagar à vista, mas descobriu que o banco oferece uma aplicação financeira que rende 1% ao mês. Após fazer os cálculos, Maria concluiu que, se pagar a primeira parcela e, no mesmo dia, aplicar a quantia restante, conseguirá pagar as duas parcelas que faltam sem ter que colocar nem tirar um centavo sequer. Quanto Maria reservou para essa compra, em reais?
A) 1.450,20
B) 1.480,20
C) 1.485,20
D) 1.495,20
E) 1.490,20
29- Prolongando-se os lados de um octógono convexo ABCDEFGH, obtém-se um polígono estrelado, conforme a figura.
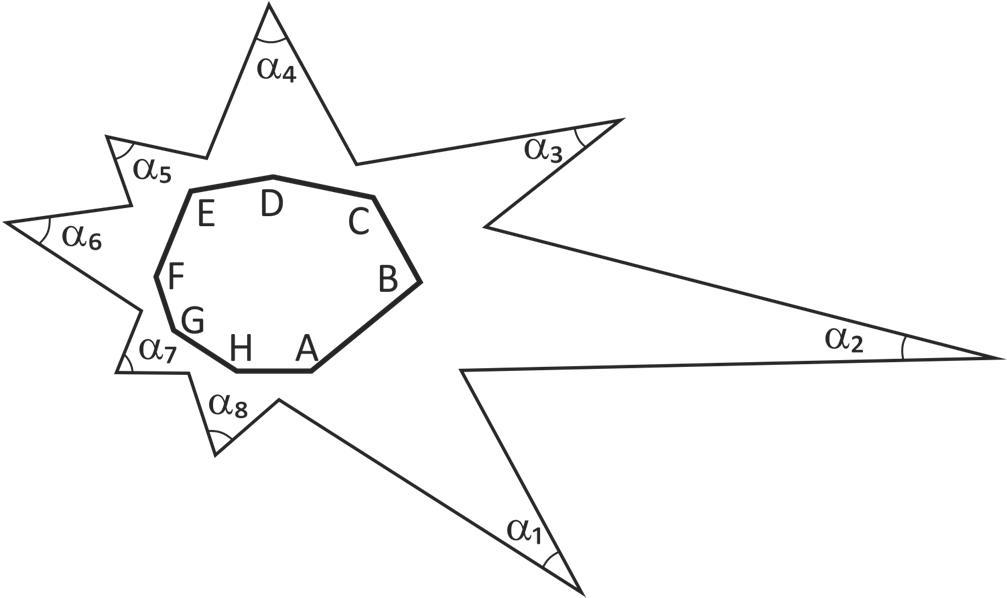
A soma ɑ1 + ...+ ɑ8 vale :
A) 180°
B) 360°
C) 540°
D) 720°
E) 900°
33- O quadrilátero da figura está inscrito em uma circunferência de raio 1. A diagonal desenhada é um diâmetro dessa circunferência.
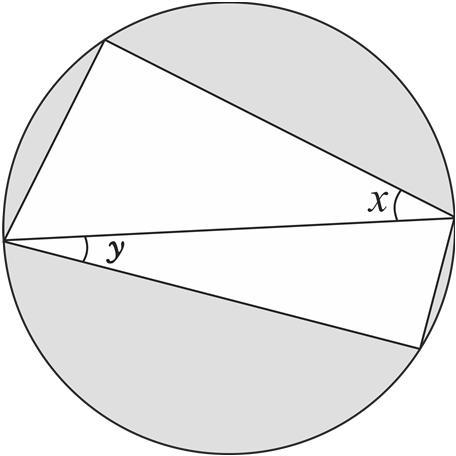
Sendo x e y as medidas dos ângulos indicados na figura, a área da região cinza, em função de x e y, é:
A) π + sen(2x) + sen(2y)
B) π - sen(2x) - sen(2y)
C) π - cos(2x) - cos(2y)
D) π -[cos(2x) + cos(2y)]/2
E) π + [sen(2x) + sen(2y)]/2
34- Dois atletas correm com velocidades constantes em uma pista retilínea, partindo simultaneamente de extremos opostos, A e B. Um dos corredores parte de A, chega a B e volta para A. O outro corredor parte de B, chega a A e volta para B. Os corredores cruzam)se duas vezes, a primeira vez a 800 metros de A e a segunda vez a 500 metros de B. O comprimento da pista, em metros, é
A) 1000
B) 1300
C) 1600
D) 1900
E) 2100