

- Jogo pega varetas: varetas vermelhas, azuis, verdes, amarelas e pretas; - Papel impresso com o ciclo trigonométrico; - Lápis e borracha; - Papel para anotações contendo uma tabela com as cores das varetas.
- Consolidar as habilidades cognitivas necessárias para a transformação das medidas dos ângulos no ciclo trigonométrico, de graus para π radianos; - Retomar as operações fundamentais no campo dos números racionais (representação fracionária); - Desenvolver habilidades elementares da trigonometria básica (ciclo trigonométrico).
Grupos com quatro alunos.
Segundo ano do ensino médio.
O jogo pega varetas trigonométrico é composto pelo jogo pega varetas com adaptações quanto aos valores de suas varetas, conforme especificado a seguir:
- Preta: 2π; - Vermelha: π/2; - Amarela: π/3; - Azul: π/4; - Verde: π/6.
As respectivas duplas de cada grupo iniciam o jogo em sentido horário e o feixe de varetas será lançado sob uma mesa plana. Cada jogador, na sua vez, fará a retirada de uma varetas sem que se mova as demais e caso isso ocorra o jogador perderá sua vez passando ao próximo jogador. Considerando que cada cor de vareta tem um valor em π radiano, vencerá o jogo a dupla que conquistar a maior soma em π radianos e consequentemente der mais voltas no cíclo trigonométrico. Para que os alunos consolidem a transformação das medidas dos ângulos de graus para π radianos, o ciclo trigonométrico terá suas medidas em graus, permitindo assim que os mesmo ao final da partida do jogo efetuem os cálculos para as conversões e definição do vencedor.
1. Cada jogador colocará seu nome nas folhas com ciclo trigonométrico impresso e a tabela para anotações. As medidas dos ângulos serão em graus.
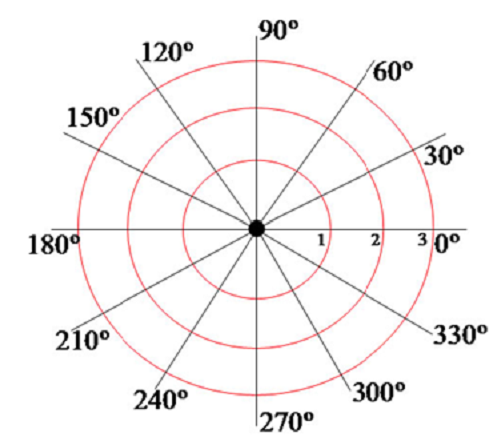
2. Após se organizarem em duplas será realizado um sorteio para definição da dupla que começara à partida.
3. Seguindo as regras do jogo, inicia-se a partida no sentido horário, pelo participante à esquerda do jogador que soltou as varetas no centro da mesa.
4. Na sua vez, o jogador tenta retirar uma vareta da cor que lhe parece mais conveniente. Se ele retirou uma vareta vermelha, por exemplo, registra nas suas anotações pessoais a cor e o valor correspondente a vareta conquistada e volta a retirar uma nova vareta enquanto consiga efetuar a retirada de maneira correta. O jogador passará a vez se ao retirar uma vareta e as demais mexerem.
5. No final da partida, cada jogador fará os cálculos relacionados às varetas obtidas em π radianos para efetuar a somatória final da dupla. Os resultados das duplas serão convertidos de π radianos para graus.
6. Ganhará o jogo a dupla cuja somatória resultar um número maior de voltas no ciclo trigonométrico.
O jogo "Pega varetas trigonométrico" como estratégia de ensino para trigonometria permite problematizações. Seguem algumas possibilidades:
(1) Representar a pontuação conquistada por meio de expressões numéricas envolvendo as operações fundamentais.
(2) Organizar os resultados obtidos de cada dupla em um gráfico de barras, para saber qual dupla obteve maior pontuação no jogo. Lembre-se que π=3,14.
(3) Organizar os resultados obtidos de cada dupla realizando o comparativo com as demais duplas para analisar qual deu volta no círculo trigonométrico.
(4) Pensar em situações como: A dupla A conquistou em sua partida do “Pega varetas trigonométrico” 2385°, enquanto a dupla B somou 1620°. Quantas varetas a mais e em que cores a dupla B deveria ter conquistado para ficar em primeiro lugar?
(4.1) Para resolver o problema da dupla B existem outras formas de combinar as varetas necessárias? Se sim, cite algumas.


