

- Pequenos saquinhos com arroz ou outro objeto, marcados de um lado com números e do outro, com figuras geométricas;
- Folha Modelo com as figuras geométricas;
- Caneta, lápis, tesoura, borracha.
- Trabalhar a concentração e a coordenação motora;
- Reconhecer as figuras planas e calcular os valores de suas áreas;
- Resgatar e consolidar alguns conceitos matemáticos importantes utilizados no cálculo da área das figuras;
- Estimular o cálculo mental e a criação de estratégias;
- Fazer com que os alunos façam suas próprias descobertas durante o jogo;
- Trabalhar jogos na perspectiva da “Etnomatemática”.
- Grupos de 3 a 6 alunos.
- 8º Ano do Ensino Fundamental II.
- Cada grupo receberá 13 peças (saquinhos), sendo 12 marcadas com figuras geométricas e números e uma “neutra” (N);
- Cada integrante do grupo contará com uma folha modelo (Exemplificada a seguir).
1º - Quem começa?
Em uma mesa plana, dispor as peças (saquinhos) de forma que a parte numérica esteja voltada para baixo;
Misturar as peças e cada jogador deve pegar uma. Começa o jogador que tirar o maior número na primeira retirada. O sentido que o jogo irá tomar depende dos dois outros jogadores, que estão à direita ou a esquerda do jogador, aquele que retirou o segundo número maior dará continuidade ao jogo.
2º - Desenvolvimento do Jogo
- Após ter definido quem começa a rodada, dispor as peças de forma que a parte geométrica esteja voltada para baixo;
* A primeira rodada será exclusiva para definir quais figuras o jogador irá efetuar o cálculo da área.
- Para iniciar, pegue a peça neutra com uma das mãos e arremesse para cima com o objetivo de pegar outras duas peças que estão sobre a mesa;
- Marque na folha modelo o par de figuras que corresponde ao desenho nas peças. Devolva as peças a mesa e misture, os próximos jogadores irão fazer o mesmo processo;
- Assim que todos escolherem as suas respectivas figuras, irá encontrar na folha modelo uma tabela indicando uma expressão algébrica correspondente a figura. Verifique e identifique em qual fórmula deverá ser substituída a expressão;
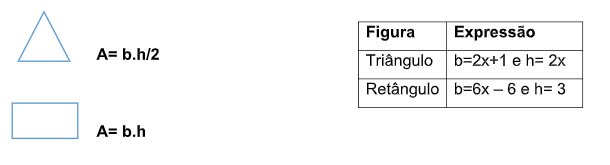
* A segunda rodada será exclusiva para definir os valores de “X” que serão atribuídos a cada expressão gerada.
- Dispor as peças de forma que a parte numérica esteja voltada para baixo;
- O jogador que iniciará a segunda rodada será o mesmo que começou o jogo. Ele irá realizar o procedimento de pegar a peça neutra e arremessar sem deixar cair, só que desta vez, ele pode pegar quantas peças ele conseguir, porém dentre as peças, ele terá que escolher qual valor se encaixa melhor nas expressões geradas de modo que consiga um maior valor de área.
- Os demais jogadores, realizarão o mesmo procedimento.
OBS: Quando o jogador deixar cair a peça neutra, ele terá somente a opção de escolher rapidamente uma peça, não tendo as opções de escolhas que teria o jogador que conseguiu conquistá-la.
- Ganha a partida o jogador que possuir o maior valor de área (m²). Para isso, ele deve somar as duas áreas calculadas e comparar com os demais participantes.
Caso houver empate nos valores, o desempate será de acordo com a seguinte ordem:
1º- Maior área círculo;
2º- Maior área triângulo
3º- Maior área trapézio;
4º- Maior área quadrado;
5º- Maior área losango;
6º- Maior área retângulo.
1) Quantos pares diferentes de figuras podemos formar no jogo?
2) É possível que a área dê um valor negativo? Justifique sua resposta.
3) É possível calcular o valor do perímetro sabendo o valor da área da figura e as informações dadas pelo jogo? Se sim, calcule.
4) Quais conteúdos matemáticos estão presentes no jogo?
5) Troque as folhas “modelo” entre os jogadores, observando e discutindo os métodos utilizados na resolução do problema.

* Os valores das expressões não são fixos, podendo ser alterados conforme a necessidade.



Fonte: Arquivo pessoal, 2018.